A Dinâmica dos Trânsitos de Vénus
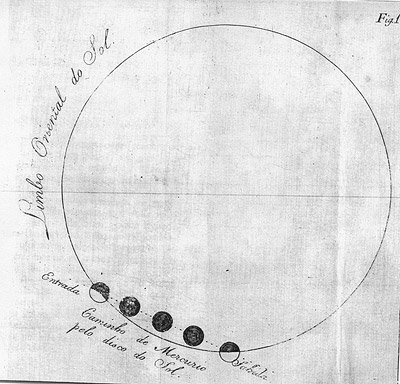
Gravura publicada no periódico português Jornal Enciclopedico Dedicado à Rainha N. Senhora, em Junho de 1789, relativa ao trânsito de Mercúrio de 5 de Novembro desse ano. Note-se como era desproporcionada a representação do disco de Mercúrio.
Tome-se o caso de Vénus como exemplo. Como este planeta descreve uma órbita menos ampla que a da Terra, o seu período é menor, tal como o prevê a Terceira Lei de Kepler. Na realidade, esse período, o «ano» de Vénus, dura 224,701 dias, enquanto o ano terrestre dura 365,256 dias. Por isso, Vénus ultrapassa periodicamente a Terra. Para o perceber melhor, imaginemos que os dois planetas são atletas às voltas, em duas pistas ovais concêntricas. O atleta interior, Vénus, demora menos tempo a dar uma volta à pista que o atleta exterior, a Terra. Por vezes, ultrapassa-o. Depois de o fazer, continua a ganhar terreno. Até que, passado algum tempo, volta a surgir por trás do atleta exterior. A cena repete-se periodicamente. Imaginemos que Vénus está, neste momento, a ultrapassar a Terra. Quando tempo demorará até voltar a surgir por detrás desta, para a ultrapassar de novo? As contas parecem difíceis, mas não o são. Primeiro, calcula-se a frequência de translação de cada planeta. Ela é dada pelo inverso dos períodos orbitais, que são 224,701 dias no caso de Vénus e 365,256 dias no caso da Terra, como vimos acima. Assim, mantendo seis algarismos significativos para os cálculos, temos a frequência 1/224,701 = 0,00445036 para o caso de Vénus e 1/365,256 = 0,00273781 para o caso da Terra. O que estes números querem dizer é que Vénus percorre aproximadamente 0,00445036 da sua órbita em 1 dia (24 horas) e que a Terra percorre apenas 0,00273781 da sua no mesmo espaço de tempo. Fazendo a diferença encontra-se 0,00171255. Essa é a fracção de órbita que Vénus ganha à Terra por dia. Para calcular quantos dias demorará a ganhar à Terra uma rotação completa, ou seja, quanto tempo demora a reencontrá-la, é preciso calcular o inverso desta quantidade, ou seja:T = 1/0,00171255 = 583,924. Este valor representa o tempo, em dias, que medeia entre duas passagens consecutivas de Vénus pela Terra, ou seja, duas conjunções inferiores. Chama-se-lhe período sinódico e é muito aproximadamente igual a 584 dias.
Nas civilizações antigas este período era muito importante, pois significa que Vénus, o planeta mais conspícuo, aparece exactamente na mesma posição no céu com intervalos de 584 dias. Assim, se em certo altura ele começava a ser visto no céu do crepúsculo, sabia-se que passados esses tantos dias haveria de aparecer exactamente na mesma posição e à mesma hora. Os Maias davam-lhe tanta importância que o período sinódico de Vénus, ao que se pensa, desempenhou um papel central na construção do calendário desse povo centro-americano. Já percebemos que, de 584 em 584 dias, o planeta Vénus está em conjunção inferior com a Terra. Porque razão não se dá um trânsito nessas alturas e não vemos pois Vénus atravessar-se sobre o Sol com a frequência correspondente?
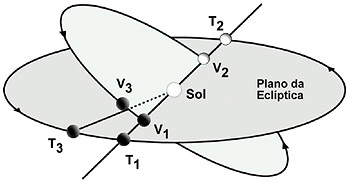
O plano de órbita da Terra é tão importante em todo este processo e em toda a astronomia observacional que recebe um nome. Chama-se-lhe plano da eclíptica. E a intersecção da esfera celeste com o plano de órbita da Terra chama-se eclíptica. Para um observador sobre o nosso planeta, a eclíptica pode ser descrita, equivalentemente, como a linha imaginária que o Sol parece descrever na esfera celeste ao longo do ano, e o plano da eclíptica será aquele que essa linha descreve. A razão desse nome é os eclipses registarem-se quando a órbita da Lua a leva ao plano da eclíptica. O mesmo se pode dizer em relação a Vénus e a Mercúrio. Os trânsitos dão-se quando esses planetas estão entre nós e o Sol, portanto em conjunção inferior, e, além disso, no plano da eclíptica, o que acontece na linha dos nodos de cada um deles. O plano orbital de Mercúrio está inclinado de 7,0° em relação à eclíptica e o de Vénus, 3,4°. Não se trata de inclinações muito pronunciadas, mas suficientes para afastarem os planetas do alinhamento perfeito quando estes não estão na respectiva linha dos nodos.
As oportunidades de observar um trânsito são raras e têm por isso de ser bem aproveitadas. Os trânsitos de Vénus são ainda mais raros que os de Mercúrio. No século XX, por exemplo, enquanto este outro planeta se atravessou entre nós e o Sol por 14 vezes, Vénus não registou um único trânsito. Esta raridade relativa dos trânsitos venusianos deve-se, entre outros factores, a um movimento muito lento das conjugações. Expliquemo-nos. Como vimos, o período sinódico de Vénus é de 583,9236 dias e o ano terrestre compreende 365,256 dias. Daqui resulta uma coincidência curiosa: cinco períodos sinódicos de Vénus são aproximadamente iguais a oito anos terrestres. Com efeito, 5 × 583,924 = 2919,620, enquanto 8 × 365,256 = 2922,048. Isto quer dizer que de oito em oito anos os três astros encontram-se aproximadamente na mesma posição no espaço. Do que se trata aqui já não é do período sideral de Vénus, que se refere à mesma posição de Vénus visto da Terra e em relação com o Sol. Mas da mesma posição dos três astros em relação às estrelas fixas: de oito em oito anos essa posição é praticamente a mesma. «Praticamente a mesma», no entanto, não quer dizer «exactamente a mesma». Como há uma diferença de dois dias e algumas horas entre os dois números acima (2922,048 - 2919,620 = 2,428), de oito em oito anos a posição de Vénus e da Terra muda um pouco, o equivalente aos movimentos de translação de 2,428 dias.
Imaginemos que, em dado dia, se regista um trânsito de Vénus. Quer isso dizer que, nesse dia, ambos os planetas estão na linha dos nodos. Passados oito anos menos 2,428 dias, os três astros estarão em posição semelhante, portanto é possível que se registe outro trânsito, mas também é possível que as órbitas dos dois planetas nesses 2,428 dias os tenha afastado dessa linha e que já não se verifique nenhum trânsito. As contas não são muito complicadas. A partir da inclinação da órbita de Vénus, pode-se verificar que o planeta sobe cerca de 20' (minutos de arco) ou desce 24', ao passar de uma conjunção inferior para a que se regista passados 2,428 dias. Ora o disco solar tem um diâmetro aparente, visto da Terra, de cerca de 32'. De tudo isto tiram-se várias conclusões. Em primeiro lugar, é perfeitamente possível que se registe um trânsito de Vénus num momento e se registe outro passado oito anos, pois tendo-se deslocado o planeta 20' ou 24' apenas, é possível que cruze o disco solar das duas vezes. Isso explica que os trânsitos de Vénus apareçam habitualmente aos pares, como se passa com o trânsito de 2004, que é seguido de um outro daqui a oito anos, em 2012. Mas isto quer dizer também que não é possível haver um terceiro trânsito passados outros oito anos, pois nessa altura já Vénus se terá deslocado 40' ou 48' e saído necessariamente fora do disco solar, que apenas mede cerca de 32'. Finalmente, tudo isto significa que o alinhamento dos planetas se move muito ligeiramente. Em oito anos menos 2,428 dias, ambos os planetas passam de uma conjunção para uma outra e avançam muito ligeiramente nas suas órbitas. Para ambos se reencontrarem exactamente num nodo pode ser preciso esperar muitos anos. E aqui os cálculos são muito mais complicados. O que interessa é que é preciso esperar sempre 105 anos e meio ou 121 anos e meio depois de um par de trânsitos separados por oito anos. E mesmo nesse par pode falhar um dos trânsitos. Foi o que aconteceu em 1388, no trânsito falhado que antecedeu o de 1396.


 Os Space Scoops continuam a ser públicados, para consultar todos os disponiveis em Português pode seguir para a
Os Space Scoops continuam a ser públicados, para consultar todos os disponiveis em Português pode seguir para a