Como se pode determinar a massa de um buraco negro estelar?
Crédito: NUCLIO (C.Zurita). Contrariamente ao mito popular, um buraco negro não é um aspirador cósmico que eventualmente irá engolir todo o Universo.
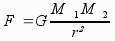
onde F é a força da gravidade, G é a constante da gravitação universal, M1 e M2 as massas de dois objectos cujos centros de massa se encontram a uma distância r.
Como vimos anteriormente o nosso Sol é uma estrela de pequena massa e jamais poderia transformar-se num buraco negro a partir de processos naturais. Contudo, vamos imaginar que num ataque de insanidade os terráqueos decidem comprimir toda a massa do Sol num raio menor do que 3 km. Nesse caso, o Sol transformar-se-ia num buraco negro. Para os planetas que circulam à sua volta não haveria qualquer alteração do campo gravítico, ou seja os planetas continuariam na mesma órbita, a distância do centro de massa dos planetas ao centro de massa do Sol (agora na forma de um buraco negro) não seria alterada, nem tampouco a sua massa. Os humanos teriam pouco tempo para vivênciar esta experiência pois a ausência da luz solar rapidamente faria desaparecer a vida na Terra. É justamente a partir do estudo da órbita de estrelas, que circulam objectos que não são visíveis, que conseguimos determinar a massa da componente compacta num binário de raios-X.
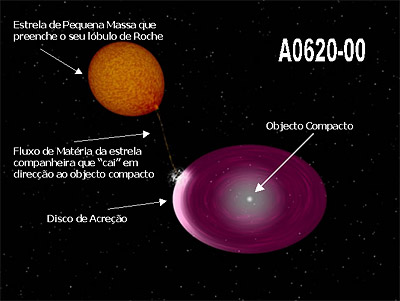
Crédito: Robert Hynes. Binário de raios-X de pequena massa A0620-00. Descoberto em 1975 tornou-se rapidamente um promissor candidato a buraco negro estelar, protótipo para o estudo de outros candidatos. Contudo a determinação definitiva da sua massa ainda não foi possível e os limites encontrados esbarram perigosamente no limite estabelecido para a massa de uma estrela de neutrões 3 Msol.
Os binários de raios-X são quase sempre detectados por serem fortes emissores de raios-X. Em alguns destes sistemas a fase de forte emissão é transiente, ou seja, tem uma curta duração. Nestes sistemas o fluxo de matéria em direcção ao buraco negro tem um comportamento espasmódico. Na maior parte do tempo a matéria proveniente da estrela vai-se acumulando nas partes mais externas do disco até que se gera uma instabilidade e o gás é subitamente acretado. Produz-se então uma erupção muito intensa e o brilho do sistema tem uma variação de cinco a dez magnitudes. É precisamente então, com a repentina aparição duma fonte brilhante no céu, num local onde antes só havia uma fonte difícil de detectar, que estes binários são descobertos. Após um período que pode durar alguns meses o sistema volta ao seu ritmo normal, uma fase a que damos o nome de quiescente. É nessa fase que se processam os estudos importantes para determinação dos parâmetros do sistema.
Ao contrário do que acontece com os binários de raios-X permanentes, em que a emissão proveniente do disco é contínua, nos binários de raios-X transientes a fonte da intensa emissão cessa e permite que outras características do sistema sejam observadas. Uma vez que o disco de acreção deixa de brilhar, a estrela companheira volta a ser visível. Os binários de raios-X transientes passam completamente despercebidos no meio de centenas de milhões de estrelas até o momento em que se produzem as erupções. O intervalo entre as erupções nestes casos é bastante longo podendo levar mesmo décadas até ocorrer uma repetição. Por essa razão só são descobertos um ou dois transientes por ano.
A função de massa
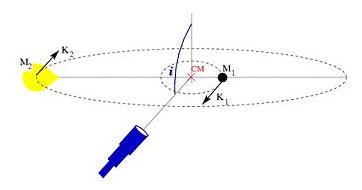
Crédito: NUCLIO (C.Zurita). Esquema dum sistema binário. O objecto compacto (de massa M1) e a estrela companheira (de massa M2) estão a orbitar em torno ao centro de massa (CM) do sistema com velocidades radiais K1 e K2 respectivamente. Como o objecto compacto é invisível temos que extrair toda a informação que precisamos da observação da estrela. A órbita forma um ângulo de inclinação i com a linha de observação.
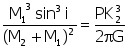
onde M1 e M2 são as massas do objecto compacto e da estrela companheira, P é o período orbital, ou seja o tempo que a estrela demora para descrever uma órbita completa, G é a constante da gravitação universal , i é a inclinação do plano da órbita do sistema com a linha de visão do observador e K2 a velocidade radial da estrela visível. Se estivermos interessados num limite inferior para a massa do objecto compacto e não exactamente a sua massa, as coisas tornam-se muito mais simples. A massa da estrela M2 não poderá ser menor que zero nem o ângulo de inclinação poderá ser maior que 90 graus pelo que a massa do objecto compacto terá que ser necessariamente maior que a quantidade que fica após de fazer i=90º e M2 =0, ou seja:
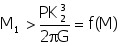
Esta quantidade, chamada função de massa ou f(M) é tremendamente importante porque nos permite obter dum modo simples uma evidência indirecta da existência dos buracos negros. Se f(M) for maior que 3 vezes a massa do Sol, a massa do objecto compacto será com certeza maior que este valor e, como vimos na primeira parte deste tema do mês, uma estrela de neutrões deve ter uma massa inferior a esse limite. Ou seja, o objecto compacto deverá ser um buraco negro! É paradoxal que a melhor evidência da existência de um dos objectos mais exóticos já imaginados pelos físicos, e o melhor exemplo da aplicabilidade da teoria da relatividade geral, tenha vindo da aplicação de simples mecânica newtoniana.
A velocidade radial da estrela
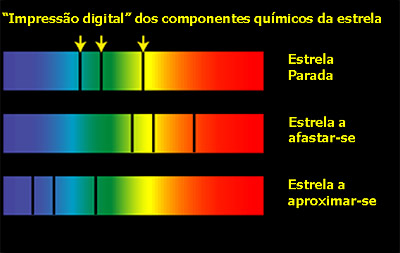
Crédito: NASA. A análise do espectro de uma estrela permite determinar a sua composição a partir do estudo das linhas espectrais. Quando a estrela está em movimento as linhas espectrais aparecem desviadas da sua posição num referencial em repouso. Se o objecto estiver a afastar-se, as linhas sofrem um desvio em direcção ao vermelho. No sentido contrário, ou seja, ao aproximar-se, o desvio é em direcção a parte azul do espectro electromagnético.
A luz da estrela é produzida por reacções nucleares no seu interior pelo que antes de viajar pelo espaço terá que atravessar a própria estrela. Uma estrela típica como o nosso Sol é composta fundamentalmente por hidrogénio mas também contém pequenas quantidades de outros elementos como hélio, carbono, azoto, oxigénio... Quando a luz os atravessa, todos estes elementos absorvem certos comprimentos de onda que dependem do elemento. Como resultado o espectro que se observa está cheio de riscas. A estrela é um emissor de luz (ou seja de ondas electromagnéticas) e está a orbitar um objecto compacto (ou seja, está em movimento). Como consequência do efeito Doppler, nos espectros obtidos por um observador na Terra, as riscas aparecerão deslocadas da sua posição normal de acordo com a velocidade da estrela em cada ponto da órbita. Em resumo, medir a deslocação das riscas do espectro da estrela, é equivalente a medir a velocidade radial da estrela. Em particular a velocidade radial máxima (K2) que a estrela atinge nos extremos da sua órbita é o parâmetro que precisamos para o cálculo da função de massa.
A função de massa diz que a massa do objecto compacto tem que ser maior que um certo limite, o que eventualmente é uma evidência da existência dum buraco negro, mas não nos dá a massa do candidato a buraco negro. Podemos no entanto ter interesse em conhecer qual é mesmo essa massa. Uma olhadela à equação diz que para isso, para além do período e da velocidade radial da estrela, necessitamos conhecer a massa da estrela companheira (M2) e o ângulo de inclinação (i).
A massa da estrela companheira
A obtenção da massa da estrela companheira é relativamente simples se já temos obtido o seu espectro. As estrelas classificam-se em diversos tipos segundo as propriedades que tenham. Cada um destes tipos tem um espectro característico, ou seja, o espectro duma estrela diz-nos a que grupo pertence e portanto como é ela e qual é a sua massa.
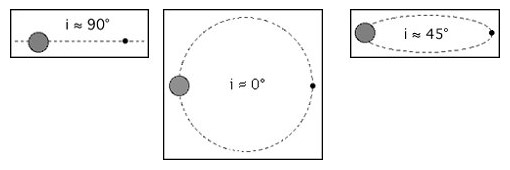
Crédito: Steven Degennaro. A figura da esquerda representa um sistema binário com uma inclinação de 90º. Neste caso, e tendo a estrela companheira a forma de uma pêra, a curva de luminosidade resultante é uma curva elipsoidal perfeita. No caso central não é possível observar qualquer variabilidade pois a estrela apresenta ao observador sempre a mesma superfície. Todos os outros casos são mais difíceis de avaliar como por exemplo os sistemas que apresentam uma inclinação de 45º.
Felizmente há uma forma de conhecer o ângulo de inclinação. Como vimos no tópico anterior, a estrela de pequena massa preenche o seu lóbulo de Roche e assume a forma de uma pêra. Isso fará com que a estrela apresente ao observador faces distintas durante o seu movimento orbital. Ou seja, a luz proveniente da estrela aparece então modulada, com dois máximos no brilho quando se apresenta ao observador “de lado”, ou seja a maior superfície, e dois mínimos quando apresenta a parte frontal e posterior de menor superfície. Como este é um efeito que depende só da geometria do sistema binário, a amplitude da modulação, chamada modulação elipsoidal, depende fortemente do ângulo de inclinação.
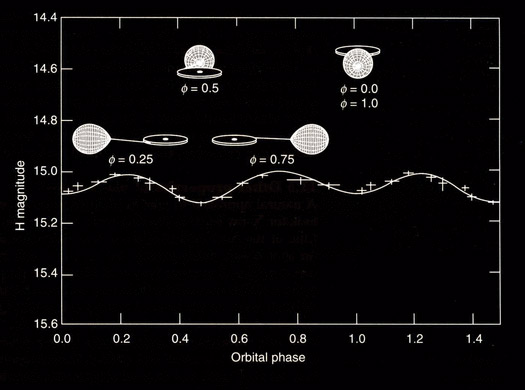
Crédito: T.Shahbaz. Nesta figura está representada a modulação elipsoidal dum sistema binário que apresenta uma inclinação de 40 graus. Pode-se verificar que as fases de maior luminosidade são aquelas em que vemos o sistema de lado. A fase orbital define a posição da estrela na sua órbita. Por convenção, chamamos fase zero àquela na qual a estrela se posiciona à frente do disco apresentando a parte posterior ao observador. As cruzes são dados reais do sistema Cen X-4. Comparando a curva real (cruzes) com o modelo (linha contínua) podemos medir o ângulo de inclinação. Cen X-4 é um dos poucos binários transitórios que parece conter uma estrela de neutrões e não um buraco negro.
Então, conhecendo a luminosidade da estrela, é relativamente simples criar curvas elipsoidais artificiais para todos os possíveis ângulos de inclinação. A comparação da curva real obtida da medição das mudanças do brilho da estrela, com as curvas teóricas, dá-nos a medida do ângulo de inclinação. Toda a informação reunida... dá-nos a desejada massa do candidato a buraco negro!
Buracos negros: Os eternos candidatos
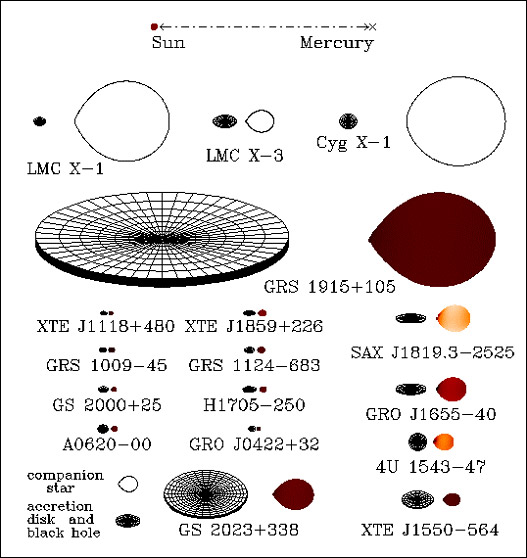
Crédito: Jerome Orosz. Este quadro apresenta 17 fortes candidatos a buracos negros estelares. Catorze são binários de pequena massa e 3 de grande massa.
Chegados a este ponto o leitor poderá perguntar: Candidato a buraco negro? Pois, a ciência é assim. Até agora temos fortes evidências mas não a prova definitiva. Podemos somente comprovar que existe naquela região um objecto compacto e que muito provavelmente será um buraco negro. Contudo a forte emissão originada no disco de acreção não nos permite observar a região mais interna. O objecto compacto está completamente inacessível. Alguns cientistas mais cépticos afirmam mesmo que o nosso conhecimento acerca da equação de estado de uma estrela de neutrões não é ainda o suficiente para garantir que elas não possam ter mais do que 3 Msol. Mas contra essa argumentação existe uma forte evidência experimental. Todas as estrelas de neutrões que conhecemos têm massas inferiores a 1,5 Msol. Poderá ainda tratar-se de um objecto estranho que a ciência ainda não previu. A prova definitiva viria se conseguíssemos comprovar a presença de um horizonte de eventos, característica exclusiva de um buraco negro.
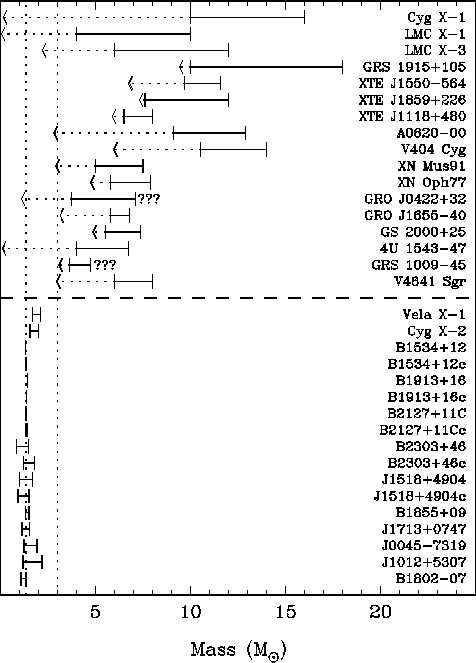
Crédito: J.Orosz. Na parte superior da figura estão alguns dos mais importantes candidatos a buracos negros e a indicação das suas massas. Na parte inferior são sistemas onde o objecto compacto é uma estrela de neutrões. Facilmente se verifica que neste último caso as massas encontram-se todas num intervalo inferior a 1,5 Msol.
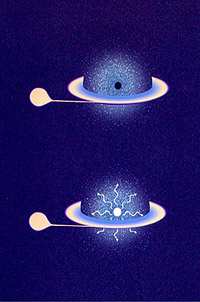
Crédito: Harvard Smithsonian Center for Astrophysics. Visão de artista de dois sistemas binários onde uma das componentes é um objecto compacto. No esquema superior o objecto compacto é um buraco negro e no inferior uma estrela de neutrões. A distinção entre estes dois sistemas pode ser feita através da observação da sua emissão em raios-X. Por não possuir um horizonte de eventos a estrela de neutrões emitirá mais radiação do que o sistema contendo um buraco negro.
O grande problema é que o número de sistemas conhecidos é muito pequeno e uma análise estatística que permita diminuir as margens de erro ainda não é possível.
E se o buraco negro não pertencer a um sistema binário será possível descobrir a sua existência? Os buracos negros existentes nos centros das galáxias não pertencem a sistema binários, como podemos medir a sua massa? Já ouvimos falar dos buracos negros estelares com massas que podem atingir 14 Msol e dos gigantescos buracos negros nos centros das galáxias com massas de milhares ou mesmo milhares de milhões de vezes a massa do Sol. Não existem buracos negros com massas intermédias? Este será o tema do próximo tópico: Buracos negros “mini” e “super”.


 Os Space Scoops continuam a ser públicados, para consultar todos os disponiveis em Português pode seguir para a
Os Space Scoops continuam a ser públicados, para consultar todos os disponiveis em Português pode seguir para a