Um resultado essencial da relatividade restrita é a relação entre massa e energia. O postulado de Einstein sobre a constância da velocidade da luz no vácuo, para todos os observadores inerciais, implica que nada se pode mover mais rápido do que a luz. Se usamos a energia para acelerar uma partícula ou uma nave espacial, a sua massa efectiva (inércia) aumenta, tornando-se cada vez mais difícil aumentar a sua velocidade. Não é possível que a nave, ou a partícula, atinja a velocidade da luz pois isso implicaria o uso de uma quantidade infinita de energia. Neste quadro, torna-se clara a equivalência entre massa e energia expressa pela mais célebre de todas as equações físicas: E=mc².

Entre as consequências importantes desta lei estão os fenómenos de cisão nuclear (do urânio) nos reactores nucleares e de fusão (de átomos de hidrogénio) no interior das estrelas. Em ambos os casos há uma perda de massa que é convertida em energia de acordo com a famosa equação. Em 1939, com o início da II Guerra Mundial, um grupo de cientistas, tomando consciência do poder da energia nuclear, e receando a eminência de uma bomba atómica alemã, persuadiram Einstein a escrever uma carta ao Presidente Franklin D. Roosevelt apelando para que os Estados Unidos iniciassem um programa de investigação nuclear. Mas o certo é que os preparativos para a bomba atómica americana, que se realizaram no âmbito do projecto Manhattan e levaram à bomba lançada em Hiroshima e Nagasaki em 1945, só começaram a sério depois do ataque a Pearl Harbor, cerca de dois anos mais tarde.

O pensamento mais feliz da minha vida

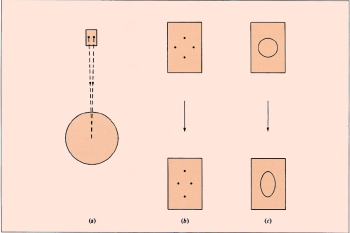
Embora a teoria da relatividade restrita tenha permitido estender a relatividade do movimento às leis do electromagnetismo, não era compatível com a lei de Newton da gravitação. Esta lei dizia que se a distribuição de matéria mudasse numa certa região do espaço, a mudança correspondente do campo gravitacional seria sentida instantaneamente em qualquer outra parte do universo. Isto não só significava que poderíamos enviar sinais mais rápidos do que a luz, mas exigia também um Tempo Absoluto já abolido pela teoria da relatividade. Einstein estava consciente deste problema quando, no Outono de 1907, Johannes Stark lhe pede para contribuir com um artigo de revisão sobre o princípio da relatividade para o seu Jahrbuch der Radioaktivität und Elektronik. Por essa altura, Einstein começava a ficar insatisfeito com a limitação da relatividade aos movimentos inerciais e ansiava por estendê-la a todos observadores. Nessa época, Einstein ainda trabalhava na Repartição das Patentes de Berna, quando teve “o pensamento mais feliz” da sua vida, como revelou ao seu colega das patentes e amigo Michele Besso. A igualdade entre a massa inercial e a massa gravitacional só poderia ser uma indicação de uma conexão íntima entre a inércia e a gravidade. Alguém numa caixa fechada não é capaz de distinguir se está em repouso num campo gravítico ou se está acelerado numa nave espacial no espaço livre. A esta conexão entre movimento acelerado e gravidade, Einstein chamou “princípio da equivalência”. Mais tarde Einstein haveria de descrever esse momento portentoso na sua lição na Universidade de Kyoto em 1922: “De repente, um pensamento assaltou-me: se uma pessoa cai em queda livre não sente o seu próprio peso. Fiquei abismado. Este simples pensamento provocou-me uma profunda impressão. Impeliu-me para uma teoria da gravitação.” Com base neste novo princípio acreditou que seria capaz de construir uma teoria que substituiria a teoria da gravidade de Newton, e ligou o problema da gravidade com o problema da extensão da relatividade a todos os observadores. É nesse artigo de 1907 que Einstein publica pela primeira vez as suas reflexões sobre a a relação entre o princípio da relatividade e a gravitação. Mas só volta a pensar nestes problemas quando estava na Universidade alemã de Praga como professor catedrático de física teórica, em 1911.

Tanto o espaço euclideano como o espaço-tempo da relatividade restrita são espaços planos. Ao procurar compatibilizar a interacção gravitacional com as ideias da relatividade restrita, Einstein é levado, ao fim de uma luta intelectual intensa, a renunciar ao espaço-tempo plano. Na presença de um campo gravítico é necessário incluir todos os tipos de movimentos relativos e não só os movimentos uniformes. Como generalizar o princípio da relatividade a todos os observadores de um campo gravítico? Vejamos, numa linguagem simples, quais as considerações que orientaram o pensamento de Einstein. Começo pelo carácter universal da gravitação. A interacção gravitacional tem uma natureza única entre todas as forças: todos os corpos caem ao longo da mesma trajectória espacial independentemente da sua massa e da sua constituição. Este facto sugere que a gravidade não é realmente uma força mas uma propriedade geométrica do espaço ou, no contexto da relatividade, do espaço-tempo. Neste ponto surge a ideia revolucionária de Einstein: os observadores em queda livre num campo gravítico identificam-se com os observadores inerciais da relatividade restrita no que diz respeito às suas observações locais. Mas, ao contrário da relatividade restrita, dois observadores em queda livre não mantêm uma velocidade uniforme entre si devido aos efeitos não locais do campo gravítico. Realmente, dois corpos em queda livre à superfície da Terra não descrevem trajectórias exactamente paralelas pois, sendo o campo central, as trajectórias convergem para o centro de massa, embora, a uma escala local, as trajectórias sejam quase paralelas (ver figura junta). Para justificar estas diferenças face à relatividade restrita, Einstein identifica a gravidade com uma modificação em relação à geometria euclideana: a gravitação produz uma curvatura do espaço-tempo. As linhas do Universo (trajectórias no espaço-tempo) dos observadores em queda livre serão as geodésicas deste espaço-tempo curvo. Claro que agora as geodésicas já não são linhas rectas, como no espaço plano, mas sim as linhas “mais direitas” que o espaço-tempo curvo admite.

Ao voltar a Zurique em 1912, como professor de física teórica na sua alma matter, a Politécnica de Zurique, Einstein mergulha profundamente no estudo das geometrias do espaços curvos (riemannianos) com a ajuda do seu antigo colega, e agora director da faculdade, Marcel Grossmann. Em 1913, Einstein e Grossmann escrevem um artigo no qual avançam esta ideia simples: o que nós pensamos serem as forças gravitacionais não é outra coisa senão a expressão da curvatura do espaço-tempo. Mas nesse trabalho não conseguiram encontrar as equações que relacionam a curvatura do espaço-tempo com a massa e a energia que nele existem.

Einstein continua a trabalhar neste problema quando vai para a Universidade de Berlim, em 1914, a convite de Max Planck e Walter Nernst. Einstein discutiu as suas ideias com o famoso matemático David Hilbert durante uma visita à Universidade de Gotinga no verão de 1915, e Hilbert “descobre” as equações do campo gravítico alguns dias antes de Einstein. Isso criou algum mal-estar entre os dois homens, mas foi ultrapassado quando Hilbert reconheceu que os créditos da descoberta deviam ser atribuídos a Einstein por inteiro. Em 1997, a disputa sobre a prioridade das equações de campo da gravitação chegou a uma conclusão final na sequência de uma investigação de L. Corry, J. Renn e J. Stachel, publicada na revista Science, Vol. 278, de 14 de Novembro, com o título: “Belated Decision in the Hilbert-Einstein Priority Dispute”. Analisando novos arquivos com as provas originais do manuscrito enviado por Hilbert ao Journal of the Scientific Society of Göttingen, com data de recepção de 16 de Dezembro de 1915, foi possível provar que Einstein não poderia ter plagiado o trabalho de Hilbert, e foi igualmente possível verificar que Einstein deduziu as suas correcções correctamente, enquanto a dedução de Hilbert só foi corrigida depois de Einstein ter publicado as suas equações.

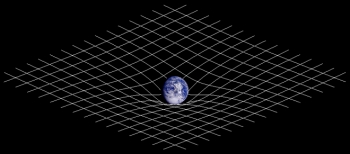
Ao descrever o campo gravítico através da curvatura do espaço-tempo, a teoria geral da relatividade transforma o espaço-tempo de um palco passivo onde os acontecimentos físicos decorrem num participante activo na dinâmica do cosmos.

Os dez anos seguintes foram anos de recepção, afirmação e sucesso da teoria. Em 1918 surgiram os primeiros dois livros devotados à relatividade geral, um em Londres por Eddington, e outro em Berlim por Herman Weyl. A 29 de Maio de 1919 o encurvamento dos raios luminosos rasando o Sol foi medido na Ilha do Príncipe e no Sobral (Brasil) durante um eclipse solar, graças ao zelo de Eddington e do Astrónomo Real britânico Frank Dyson. As previsões da teoria de Einstein foram publicamente confirmadas no famoso encontro da Royal Society em Londres a 6 de Novembro de 1919. No dia seguinte, no cabeçalho do jornal londrino Times podia ler-se: “Revolução na Ciência/ Nova Teoria do Universo/ Ideias Newtonianas Abandonadas.”

A Primeira Guerra Mundial tinha terminado. O mundo estava cansado e desiludido, e à procura de novos ideais. A teoria de Einstein com as suas ideias bizarras sobre a curvatura do espaço(-tempo) captou a imaginação da opinião pública, embora muito poucas pessoas a compreendessem. Apareceram então inúmeros artigos de divulgação em jornais e em revistas filosóficas que entusiasmaram o público culto e tornaram a relatividade num tema de conversação obrigatório. O próprio Einstein escreveu um longo artigo no Times em finais de 1919, procurando explicar a teoria aos leigos. Na capa da revista noticiosa Berliner Illustrirte de 14 de Dezembro de 1919 a sua fotografia é publicada com a legenda: “Uma nova grande figura da história mundial." Einstein torna-se então um pensador célebre em todo o mundo e a sua opinião é solicitada para os mais variados assuntos. Os Estados Unidos recebem-no com pompa e circunstância e o seu nome passa a ser pronunciado com reverência, acabando por adquirir o significado do génio. Nem todos, porém, aplaudiram o triunfo de Einstein. Alguns membros da comunidade científica e outras pessoas movidas por razões mais políticas do que científicas moveram-lhe uma guerra sem quartel, afirmando que a sua teoria era totalmente incompreensível e inútil.

O Renascimento da Relatividade Geral

Depois de ter sido considerada durante muito tempo uma teoria difícil e esotérica, sem aplicação aos restantes domínios da física, limitada a descrever pequenas correcções à teoria da gravitação de Newton, a relatividade geral tornou-se finalmente uma teoria popular, tendo ganho hoje um lugar seguro entre os curricula dos cursos de física e de matemática da maioria das universidades.

Este êxito estrondoso foi naturalmente suscitado pelos importantes desenvolvimentos teóricos iniciados nos anos 60, bem como pelas retumbantes observações astronómicas que se verificaram no mesmo período. Foi a combinação destes dois tipos de contribuições que provocou um verdadeiro renascimento da relatividade geral, ao mesmo tempo que se reforçou a sua aplicação à Astrofísica e à Cosmologia.

Vejamos quais os desenvolvimentos experimentais e teóricos que mais contribuíram para o renascimento da relatividade geral.

A 9 de Março de 1960, o corpo editorial do periódico científico Physical Review Letters recebe o artigo de Pound e Rebka, intitulado “O Peso Aparente dos Fotões". O artigo descreve a primeira medida laboratorial bem sucedida da mudança de frequência ou do comprimento de onda da luz por influência do campo gravítico da Terra.

Alguns meses mais tarde, no número de Junho de 1960 da revista científica Annals of Physics surge um artigo assinado pelo físico-matemático inglês Roger Penrose intitulado “Tratamento Spinorial da Relatividade Geral”. Embora se tratasse de um artigo com um formalismo matemático pesado, delineava uma técnica de cálculo extremamente elegante para resolver alguns problemas de relatividade geral. Este foi um dos primeiros passos dados no sentido de tornar mais simples muitos dos morosos e complexos cálculos relativistas.

Ainda no ano de 1960 têm início as observações levadas a cabo pelos astrónomos americanos Thomas Mathews e Allan Sandage, com o telescópio de 200 polegadas de Monte Palomar na Califórnia, da fonte de rádio 3C48 (objecto número quarenta e oito do terceiro catálogo de Cambridge de fontes de rádio). Estavam interessados em estudar a radiação visível emitida por esta fonte e, para isso, tiraram uma chapa fotográfica da zona do céu à roda da 3C48. Esperavam encontrar um enxame de galáxias com a localização da fonte de rádio, mas não foi isso que observaram. A análise da chapa fotográfica parecia indicar que o objecto afinal tinha as dimensões de uma estrela, mas não era uma estrela vulgar, pelo menos nada comparável a qualquer estrela conhecida. O seu espectro tinha cores bastante invulgares, e apresentava grandes e rápidas variações de brilho. Era pois uma fonte de rádio, que parecia do tipo “estelar” (apesar das estrelas ordinárias não serem fontes intensas de rádio) mas que pelo tipo e variabilidade do seu espectro não parecia ser exactamente uma estrela. Daí que fosse designada fonte de rádio quase estelar ou quasar.

A descoberta dos quasares catapultou a relatividade geral imediatamente para a fronteira da astronomia. Foram entretanto descobertos objectos semelhantes, como o 3C273. E em 1963 Martin Schmidt do Observatório de Monte Wilson descobriu que as riscas do espectro de emissão do 3C273 apresentavam um deslocamento de 16 por cento no sentido dos comprimentos de onda mais altos. Para o 3C48 foi medido posteriormente um deslocamento para vermelho ainda maior, da ordem dos 30%. Em 1929, Edwin Hubble tinha anunciado que as galáxias distantes se afastam com velocidades proporcionais às suas distâncias. Este sistemático deslocamento para o vermelho no espectro das galáxias distantes é ainda hoje interpretado como uma expansão do Universo. Os grandes deslocamentos para o vermelho dos espectros dos quasares mostram que eles se afastam de nós com grandes velocidades, cerca de 30 por cento da velocidade da luz no caso do 3C48, a que corresponde uma distância da ordem de 6 biliões de anos-luz. Estando os quasares tão distantes seria de esperar que fossem objectos com fraco brilho. Mas, pelo contrário, os quasares são objectos extremamente brilhantes, tanto na parte visível como na das ondas de rádio do espectro. Portanto, a sua luminosidade intrínseca deve ser enorme. O 3C48 é cerca de 100 vezes mais luminoso que a nossa galáxia.

Qual a origem de uma fonte tão poderosa? Como se explicam as suas rápidas variações de brilho? À escala cósmica, a gravidade é a interacção dominante, por isso é provável que a resposta a estas perguntas esteja na existência de campos gravitacionais extraordinariamente intensos, o que pode implicar concentrações imensas de massa, talvez com milhões de vezes a massa solar, confinadas a uma região do espaço que não deve ultrapassar uma hora-luz (aproximadamente igual ao diâmetro da órbita de Júpiter).

A descoberta dos quasares deu origem à criação de uma nova área da física. Em Dezembro de 1963, em Dallas, Texas, teve lugar o primeiro simpósio sobre esta nova disciplina designada Astrofísica Relativista. Para esta conferência foram convidados astrónomos, físicos e matemáticos, de modo a proporcionar um debate alargado, capaz de reunir as experiências e os conhecimentos diversificados destas três áreas do saber. Segundo o testemunho de alguns dos seus participantes, a atmosfera reinante era de grande nervosismo e excitação. Em parte pelo recente assassinato do presidente John Kennedy, mas em boa medida por que se tratava de uma experiência nova de comunicação entre cientistas de áreas diferentes e porque se vivia então um período de grande euforia científica.

Algum tempo mais tarde, no final do ano de 1967, os astrónomos da Universidade de Cambridge Jocelyn Bell e Anthony Hewish descobriram um novo tipo de estrela, chamada pulsar devido à emissão regular de impulsos de rádio. Pensa-se que os pulsares são estrelas imensamente compactas, tão densas que os seus diâmetros não ultrapassam poucas dezenas de quilómetros, e que podem rodar muitas vezes num segundo. A compactificação nestas estrelas é tão grande que destrói os seus átomos e os reduz a um mar de neutrões. Daquilo que se conhece da matéria nuclear, estas estrelas de neutrões parecem encontrar-se à beira de um espectacular acidente catastrófico. A gravidade à superfície da estrela é tão intensa, que se uma estrela de neutrões tiver uma massa maior que três massas solares será incapaz de encontrar uma estrutura de equilíbrio, colapsando numa fracção de segundo e desaparecendo totalmente do Universo.

A explicação deste intrigante fenómeno reside na violenta curvatura do espaço que traduz a crescente intensidade da gravidade numa estrela em colapso. À medida que o raio da estrela se reduz, a curvatura do espaço à superfície da estrela rapidamente se torna suficientemente forte para encurvar os raios luminosos e retê-los em torno da estrela. Quando nem a própria luz consegue escapar ao campo gravítico da estrela esta transforma-se num verdadeiro buraco negro no espaço. No interior do buraco negro, a matéria continua a ser inexoravelmente atraída para o centro do buraco: nenhuma força do Universo parece ser capaz de parar este processo de colapso.

Os buracos negros são sem dúvida objectos de estudo fascinantes. Mas foram muito mal compreendidos durante muito tempo. Quando Chandrasekhar desenvolveu em 1931 a sua teoria das anãs brancas, mostrando que estas estrelas não poderiam ter uma massa superior a 1,4 massas solares, encontrou muita oposição por parte de Eddington. Embora a teoria das anãs brancas não se baseie na relatividade geral, depende com certeza da interacção gravitacional. Eddington percebeu claramente que uma consequência dessa teoria para as estrelas com massa suficiente era a inevitabilidade do colapso, com formação de uma singularidade do espaço-tempo, isto é, um ponto onde a curvatura se torna infinita e todas as leis físicas são violadas. Eddington considerava isto um absurdo e portanto atrasou muito a aceitação da teoria das anãs brancas entre astrónomos e astrofísicos.

Em 1939 J.R. Oppenheimer e H. Snyder calcularam o colapso de um fluido esfericamente simétrico e sem pressão usando as equações de Einstein da relatividade geral. Mostraram que não há nada nas equações de Einstein que possa evitar o colapso e a formação do buraco negro associado. Mas, mesmo depois deste resultado, o conceito de buraco negro permaneceu adormecido durante os trinta anos seguintes até à descoberta dos quasares. Há realmente dois factos que contribuíram para a retoma destas ideias. O primeiro, relaciona-se com os quasares e com a necessidade de compreender as enormes quantidades de energia emitida por estes objectos. Para explicar os intensos campos gravitacionais responsáveis pela produção de energia, Edwin Salpeter da Universidade de Cornell recorreu aos objectos estudados por Oppenheimer e Snyder. O segundo facto foi a descoberta em 1963 de uma solução das equações de Einstein por Roy P. Kerr. Kerr recorreu a um conjunto de sofisticadas técnicas matemáticas que exploram os princípios de simetria na pesquisa de novas soluções das equações de Einstein.

Quando Kerr apresentou a sua comunicação no primeiro simpósio do Texas em Astrofísica Relativista, poucos puderam acompanhá-lo devido à complexidade dos cálculos envolvidos. Mas hoje sabe-se que a solução de Kerr é a única solução para um buraco negro em rotação e a solução obtida por Schwarzschild em 1916, dois meses após a publicação da teoria de Einstein, é simplesmente um caso particular da solução de Kerr quando não há rotação.

Envolvidos com o problema dos quasares, os astrofísicos relativistas consumiram os dez anos seguintes provando esta e muitas outras características das soluções de Schwarzschild e de Kerr. Por exemplo, sabia-se que a geometria de Schwarzschild apresentava um comportamento patológico junto do chamado raio gravitacional, R=2GM/c², correspondente às dimensões do buraco negro. E uma situação semelhante ocorria com a geometria de Kerr. Ficou então provado que estes problemas eram causados por uma má escolha de coordenadas. Contudo, isso não alterou o facto da superfície correspondente ao raio gravitacional, também conhecido por raio de Schwarzschild, possuir uma propriedade especial. Foi-lhe dado o nome de “horizonte de acontecimentos” porque essa superfície funciona como uma membrana que deixa passar a informação num só sentido: para um observador exterior, todos os acontecimentos com R<2GM/c² são completamente inacessíveis. Foi esta característica do horizonte de acontecimentos que levou John Wheeler a introduzir o termo buraco negro, durante uma conferência realizada em Nova Iorque em 1967.

Para um observador que se encontre bastante afastado do horizonte, a única característica detectável do buraco negro é o seu campo gravítico. Este não se distingue do campo produzido por qualquer outro objecto com a mesma massa e momento angular. Porém, para um observador próximo do horizonte surgem fenómenos muito estranhos. O encurvamento dos raios luminosos pode ser tão grande que a luz pode ficar retida em torno do buraco seguindo uma órbita circular, com um raio R=3GM/c² no caso do buraco negro de Schwarzschild. Nos buracos negros de Kerr, a rotação dá origem a um arrastamento dos observadores em queda livre em torno do buraco tal que, se estes se encontram próximo do horizonte e seguindo uma órbita equatorial, o arrastamento em torno do buraco torna-se tão forte que nada poderá evitá-lo. Estas e muitas outras características dos buracos negros foram estabelecidas durante um período de intensa pesquisa, entre 1963 e 1974, por um conjunto de relativistas famosos que assim muito contribuiram para o renascimento da teoria. Para terminar esta exposição não podemos deixar de referir duas áreas de investigação muito actuais em relatividade: a cosmologia relativista e a detecção de ondas gravitacionais, a primeira das quais será discutida na próxima semana e a segunda já foi tema do mês no portal do astrónomo.