Space Scoops

A diversidade dos fenómenos da Natureza é tão vasta e os tesouros escondidos no Céu são tão ricos precisamente para que a mente humana nunca tenha falta de alimentos.

Mysterium Cosmographicum (1596), Kepler

As observações de Tycho Brahe sobre o movimento aparente dos planetas, apesar de não apoiarem o seu "Mistério Cosmográfico", permitiram a Kepler obter de modo empírico três leis gerais que descrevem o movimento dos planetas.

1ª Lei de Kepler As órbitas dos planetas são elipses, ocupando o Sol um dos seus focos. 2ª Lei de Kepler (ou lei das áreas) O raio vector que une o centro do Sol ao centro de cada planeta descreve áreas iguais em intervalos de tempo iguais. 3ª Lei de Kepler O quadrado do período de revolução T de cada planeta em torno do Sol é proporcional ao cubo do comprimento do semi-eixo maior a da respectiva órbita (ou seja, a3/T2 = constante).

Figura 6. A lei das áreas. Das 1ª e 2ª leis conclui-se que o movimento dos planetas não tem velocidade constante. Para que a área varrida seja proporcional ao tempo gasto a descrevê-la é necessário que a velocidade seja máxima no periélio (ponto da órbita mais próximo do Sol) e mínima no afélio (ponto da órbita mais afastado do Sol).

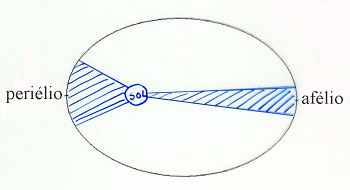
A partir das 1ª e 2ª leis, Kepler concluiu que o movimento dos planetas não tem velocidade constante. A velocidade mínima é atingida no afélio (ponto da órbita elíptica que está mais afastado do Sol) e a velocidade máxima é atingida no periélio (ponto da órbita elíptica que está mais próximo do Sol). Kepler podia agora aplicar estas novas conclusões à teoria musical das esferas. A primeira observação a fazer era a de que, tendo o planeta velocidade variável, não emitia uma nota única, sendo a nota mais aguda atingida no periélio e a mais grave no afélio. A partir da diferença entre as velocidades mínima e máxima, podia ainda calcular o intervalo musical definido pelas notas mais grave e mais aguda produzidas por cada planeta.

	Figura 7. A música das esferas de Kepler. Kepler deduziu os intervalos musicais produzidos por cada planeta. Para ele, a melodia produzida por cada planeta não era uma sequência de notas distintas, mas sim um único som eterno, a variar continuamente entre o mais grave e o mais agudo, como o som produzido por um violinista deslocando continuamente o seu dedo, sem o levantar, sobre a corda do seu violino.

A partir da 3ª lei, podia relacionar os sons produzidos pelos diversos planetas. Concluindo que os planetas mais longínquos eram mais lentos, ele entendeu que os sons produzidos seriam mais graves à medida que a distância ao Sol aumentava.

Nesta teoria, os sons produzidos pelos diversos planetas são tanto mais graves quanto maior a distância ao Sol, o centro, ao contrário dos sistemas inspirados em Ptolomeu, nos quais o som se vai tornando mais agudo à medida que a distância ao centro do sistema, nesse caso a Terra, aumenta.

O modelo de Copérnico obrigava-o a estudar o cosmos como se fosse visto a partir do Sol. Kepler efectuou cálculos com o objectivo de calcular para cada planeta o "movimento diário aparente" (o comprimento de arco percorrido num período de 24 horas) no afélio e no periélio. Por exemplo, Kepler deduziu que Saturno percorre um arco de 135 segundos por dia quando está mais perto do Sol (arco esse visto do Sol) e um arco de 106 segundos por dia quando está mais afastado do Sol. A razão 135/106 está muito próxima de 5/4, a razão entre as frequências associadas ao intervalo de terceira maior em música. Usando este método para todos os planetas, ele descobriu que as razões periélio-afélio relacionadas com quaisquer dos seis planetas são todas muito semelhantes às razões associadas a intervalos musicais consonantes. Assim, para Júpiter a razão periélio-afélio seria aproximadamente 6/5 (uma terceira menor); para Marte seria 3/2, uma quinta perfeita; para a Terra, 16/15, um meio–tom; para Vénus, 25/24, um intervalo muito próximo da coma pitagórica; para Mercúrio, 12/5, uma décima menor [2].

Os movimentos dos céus não são mais que uma eterna polifonia.

Harmonices Mundi (1619), Kepler

Na sua obra Harmonices Mundi (1619), Kepler imaginou um coro no qual Mercúrio, a voz mais aguda, seria o Soprano, Vénus e Terra os Contraltos, Marte o Tenor, enquanto que Júpiter e Saturno, as vozes mais graves, seriam os Baixos. Nesta sua teoria da música celestial, ao planeta Terra correspondia um intervalo musical de meio-tom, que ele associou ao modo eclesiástico de mi (modo frígio), levando-o a concluir que a melodia entoada pela Terra era "mi – fá – mi". Kepler fazia esta descoberta durante a Guerra dos Trinta Anos, o que o levou a pensar que a Terra produzia um lamento constante, em nome da misere e fami (miséria e fome) que reinavam na altura (nas palavras de Kepler, Tellus canit MI-FA–MI ut vel ex syllaba conjicias, in hoc nostro domicilio Miseriam et Famen obtinere).

O fim da música das esferas

O Século XVII representa uma transição crítica na história do pensamento do homem, pois marca o momento da separação entre fé e dogma religioso por um lado, e a visão mecanicista da natureza por outro.

Fludd (1574-1637) e Kepler (1571-1630) parecem ter sido os últimos a propor uma relação real entre movimentos dos planetas e notas musicais específicas. Por outro lado, o mesmo Kepler que parecia estar a perder o seu tempo em busca da quimera da música das esferas, deve ter sido o primeiro a respeitar rigorosamente dados de observações, apesar de contradizerem uma sua primeira teoria. Afinal foi em busca dessa quimera que ele deduziu as suas três leis.

Algum tempo depois, Newton (1642-1727) mostrava ao mundo que leis matemáticas universais relativamente simples presidem a natureza, podendo mesmo deduzir a partir delas as leis que Kepler tinha encontrado empiricamente.

Era o nascimento do pensamento científico, tal como hoje o conhecemos.